Problem 1.
Modular arithmetic and 2's complement representation
Most computers choose a particular word length (measured in bits)
for representing integers and provide hardware that performs various
arithmetic operations on word-size operands. The current generation
of processors have word lengths of 32 bits; restricting the size of
the operands and the result to a single word means that the arithmetic
operations are actually performing arithmetic modulo 2
32.
Almost all computers use a 2's complement representation for
integers since the 2's complement addition operation is the same for
both positive and negative numbers. In 2's complement notation, one
negates a number by forming the 1's complement (i.e., for each bit,
changing a 0 to 1 and vice versa) representation of the number and
then adding 1. By convention, we write 2's complement integers with
the most-significant bit (MSB) on the left and the least-significant
bit (LSB) on the right. Also by convention, if the MSB is 1, the
number is negative; otherwise it's non-negative.
-
How many different values can be encoded in a 32-bit word?
-
Please use a 32-bit 2's complement representation to answer the
following questions. What are the representations for
zero
the most positive integer that can be represented
the most negative integer that can be represented
What are the decimal values for the most positive and most negative integers?
-
Since writing a string of 32 bits gets tedious, it's often convenient
to use hexadecimal notation where a single digit in the range 0-9 or
A-F is used to represent groups of 4 bits using the following
encoding:
hex bits hex bits hex bits hex bits
0 0000 4 0100 8 1000 C 1100
1 0001 5 0101 9 1001 D 1101
2 0010 6 0110 A 1010 E 1110
3 0011 7 0111 B 1011 F 1111
Give the 8-digit hexadecimal equivalent of the following decimal and
binary numbers: 3710, -3276810, 110111101010110110111110111011112.
-
Calculate the following using 6-bit 2's complement arithmetic (which
is just a fancy way of saying to do ordinary addition in base 2
keeping only 6 bits of your answer). Show your work using binary
(base 2) notation. Remember that subtraction can be performed by
negating the second operand and then adding it to the first operand.
13 + 10
15 - 18
27 - 6
-6 - 15
21 + (-21)
31 + 12
Explain what happened in the last addition and in what sense your
answer is "right".
-
At first blush "Complement and add 1" doesn't seem to an obvious way
to negate a two's complement number. By manipulating the expression
A+(-A)=0, show that "complement and add 1" does produce the correct
representation for the negative of a two's complement number.
Hint: express 0 as (-1+1) and rearrange terms to get -A on one
side and XXX+1 on the other and then think about how the expression
XXX is related to A using only logical operations (AND, OR, NOT).
Problem 2.
Recall that in a N-bit sign-magnitude representation, the most significant
bit is the sign (0 for positive, 1 for negative) and the remaining
N-1 bits are the magnitude.
-
What range of numbers can be represented with an N-bit sign-magnitude
number? With an N-bit two's-complement number?
-
Create a Verilog module that converts an N-bit sign-magnitude
input into an N-bit two's complement output.
Problem 3.
Carry-select adder
In thinking about the propagation delay of a ripple-carry adder,
we see that the higher-order bits are "waiting" for their carry-ins to
propagate up from the lower-order bits. Suppose we split off the
high-order bits and create two separate adders: one assuming that
the carry-in was 0 and the other assuming the carry-in was 1. Then
when the correct carry-in was available from the low-order bits, it could be
used to select which high-order sum to use. The diagram below shows
this strategy applied to an 8-bit adder:
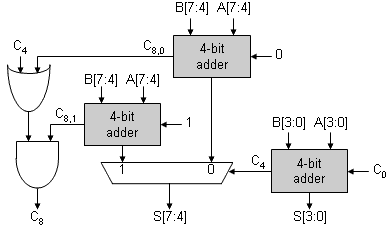
-
Compare the latency of the 8-bit carry-select adder show above to
a regular 8-bit ripple-carry adder.
-
The logic shown for C8 seems a bit odd. One might have
expected C8 = C8,0 + (C4*C8,1).
Explain why both implementations are equivalent and suggest why the
logic shown above might be prefered. Hint: What can we say about C8,1
when C8,0=1?
Problem 4.
Pipelining.
Pipelining is particular form of retiming where the goal is to
increase the throughput (number of results per second) of a circuit.
Consider the circuit diagram below; the solid rectangles represent
registers, the square are blocks of combinational logic:
Each combinational block in the diagram is annotated with it's
propagation delay in ns. For this problem assume that the registers
are "ideal", i.e., they have zero propagation delay, and zero setup
and hold times.
-
What are the latency and throughput of the circuit above? Latency is how long
it takes for a value in the input register to be processed and the result appear at the
output register. Throughput is the number of results per second.
-
Pipeline the circuit above for maximum throughput. Pipelining adds additional
registers to a circuit; we'll do this by adding additional registers at the output
and then use the retiming transformation to move them between the combinational
blocks. What are the latency and throughput of your resulting circuit?
